Point values in the game "Target"

June 2008

• Introduction
• Setup
• Graph
• Results
• Derivation
  • Flushes
  • Straights
  • Straight Flushes
  • Poker Hands
  • Miscellaneous
• About this project

Introduction

Target is a game where you draw cards to try to satisfy the target cards. Each of the cards has a separate point value, and I wondered how "true" those points were. So, my goal was to calculate the number of 6 card hands (in the game your hand limit is 5, but you draw a card and then can turn sets in) that satisfy each of the conditions and see if there was a way to derive how points were allocated. It was also a good excuse to calculate (using combinatorics) the exact number of hands that satisfy each condition, and to check those numbers using a Python script.

Setup

Target cards are 0-9 in four different suits (purple, green, red, blue) plus 1 wild suit in each number. 0 and 9 have one of each suit and all other numbers have two of each suit for a total of \(2(4+1)+8(2\cdot4+1)=82\) cards. The total number of possible hands is \({82\choose 6}=350161812\).

Graph

The x-axis represents the probability that a random 6-card hand will satisfy the target card. The y-axis is just the number of cards you have to turn in to fulfill the target card, and the color of the dot (and the corresponding text) is how many points it's worth. So, dots in the upper-left hand corner are the hardest to get and take the most cards, and you would expect these to be worth the most points (which they generally are).

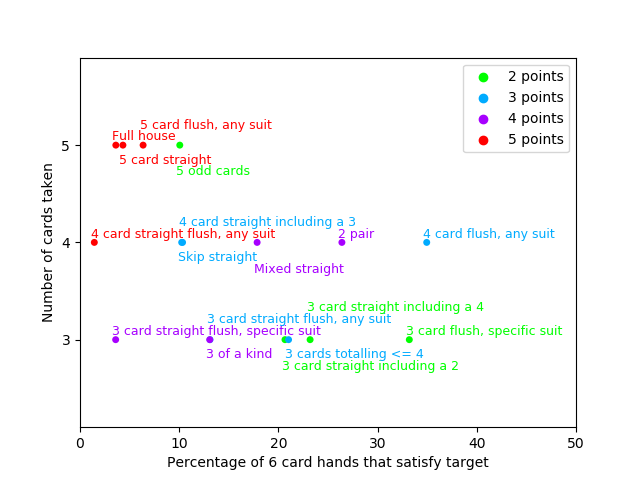
There are some interesting results here - all the 5 point targets are at the left and towards the top, as expected, but there are some interesting outliers. At 2 points, 5 odd cards seems undervalued; it's the only target that takes more than 3 cards that's only worth 2 points (and it has a pretty low probability to boot). 4 card straight including a 3 and skip straight both seem undervalued since mixed straight is more likely and is worth more points. 3 card straight including a 2 looks similarly undervalued. (or maybe 3 cards totalling <= 4 is overvalued?)

One possibility is that the designers of the game looked at the probabilities with 5 card hands instead of 6 cards as I've done. Another is that they chose to fiddle with the point values to account for the fact that certain target cards are easier to turn in together - if you have 5 odd cards you have a pretty good chance of having a skip straight, etc.

Results

I was able to calculate almost all the results symbolically. Here are the results. Click on a hand type to see the derivation of that number. These results were derived by hand (except the ones in bold) and checked with a Python script.

	Hand type	Points	Possible hands	Probability
Flush
	3 card, specific suit	2	116241489	33.197%
	4 card, any suit	3	122384088	34.951%
	5 card, any suit	5	22272138	6.361%
Straight
	3 card including a 2	2	72355734	20.664%
	3 card including a 4	2	81222993	23.196%
	3 card including a 5	2	81222993	23.196%
	3 card including a 7	2	72355734	20.664%
	4 card including a 3	3	36204327	10.339%
	4 card including a 6	3	36204327	10.339%
	5 card	5	15149349	4.326%
Straight Flush
	3 card, specific suit	4	12588978	3.595%
	3 card, any suit	3	45888079	13.105%
	4 card, any suit	5	5054955	1.444%
Poker
	2 pair	4	92445176	26.401%
	3 of a kind	4	45800298	13.080%
	Full house	5	12646280	3.612%
Misc
	5 odd cards	2	35221706	10.059%
	5 even cards	2	35221706	10.059%
	3 cards totalling \(\leq 4\)	3	73617980	21.024%
	3 cards totalling \(\geq 23\)	3	73617980	21.024%
	Skip straight	3	35894502	10.251%
	Mixed straight	4	62519949	17.855%

Derivation

Flushes

3 card flush, specific suit

Without loss of generality, let the suit be G(reen). There are 28 cards that can be G - 18 G and 10 W(ild), and so there are \(82-28=54\) cards that cannot be G. To avoid double-counting, we split up the possibilities:

• 6 card flush: \({28\choose 6}=376740\)
• 5 card flush: \({28\choose 5}{54\choose 1}=5307120\)
• 4 card flush: \({28\choose 4}{54\choose 2}=29299725\)
• 3 card flush: \({28\choose 3}{54\choose 3}=81257904\)

So the total is \(376740+5307120+29299725+81257904=\mathbf{116241489}\).
Back to table

4 card flush, any suit

We break it down by the number of wilds in the hand. Note that there are 10 wilds and 18 cards of each suit, which means there are 54 cards not in a given suit.

• 0 wilds: There are 4 choices for the suit the flush is in, and in a given suit there are \({18\choose6}+{18\choose5}{54\choose1}+{18\choose4}{54\choose2}\) possibilities, which gives \(4({18\choose6}+{18\choose5}{54\choose1}+{18\choose4}{54\choose2})=19440384\).
• 1 wild: There are 10 choices for which wild we have. We only need 3 cards in any one suit to have a flush, and since there are only 5 cards left we don't need to worry about overcounting. So there are 4 choices for a suit and \({18\choose5}+{18\choose4}{54\choose1}+{18\choose3}{54\choose2}\) choices for the cards in that suit, which gives \(10\cdot4({18\choose5}+{18\choose4}{54\choose1}+{18\choose3}{54\choose2})=53660160\).
• 2 wilds: There are \(10\choose2\) choices for which wilds we have. There are 4 cards left and we only need 2 of the same suit to make a flush, so only 1 card in each suit will fail to give a flush. There are \(18^4\) failures, so there are \({72\choose4}-18^4\) possibilities, which gives \({10\choose2}({72\choose4}-18^4)=41571630\).
• 3 wilds: There are \(10\choose3\) choices for which wilds we have, and any remaining set of cards will give a 4 card flush, so there are \(72\choose3\) possibilities, which gives \({10\choose3}{72\choose3}=7156800\).
• 4 wilds: There are \(10\choose4\) choices for which wilds we have, and any remaining set of cards will give a 4 card flush, so there are a total of \({10\choose4}{72\choose2}=536760\) possibilities.
• 5 wilds: There are \(10\choose5\) choices for which wilds we have, and any remaining set of cards will give a 4 card flush, so there are a total of \({10\choose5}{72\choose1}=18144\) possibilities.
• 6 wilds: There are \(10\choose6\) possibilities.

So, the total is \(19440384+53660160+41571630+7156800+536760+18144+210=\mathbf{122384088}\).
Back to table

5 card flush, any suit

Similarly, we break it down by the number of wilds in the hand.

• 0 wilds: There are 4 choices for the suit the flush is in, and in a given suit there are \({18\choose6}+{18\choose5}{54\choose1}\) possibilities, which gives \(4({18\choose6}+{18\choose5}{54\choose1})=1924944\).
• 1 wild: There are 10 choices for which wild we have, and 4 choices for the suit the flush is in. We need 4 out of the remaining 5 cards to be in that suit, so there are \({18\choose5}+{18\choose4}{54\choose1}\) possibilities for those cards, which gives a total of \(10\cdot4({18\choose5}+{18\choose4}{54\choose1})=6952320\).
• 2 wilds: There are \(10\choose2\) choices for which wilds we have. We need 3 cards in any one suit to give a flush and there are 4 cards left so there is no danger of overcounting. Thus, there are 4 choices for a suit and \({18\choose4}+{18\choose3}{54\choose1}\) choices for the cards in that suit, which gives a total of \({10\choose2}4({18\choose4}+{18\choose3}{54\choose1})=8482320\).
• 3 wilds: There are \(10\choose3\) choices for which wilds we have. We need 2 cards in any one suit to give a flush and there are 3 cards left so there is no danger of overcounting. Thus, there are 4 choices for a suit and \({18\choose3}+{18\choose2}{54\choose1}\) choices for the cards in that suit, which gives a total of \({10\choose3}4({18\choose3}+{18\choose2}{54\choose1})=4357440\).
• 4 wilds: There are \(10\choose4\) choices for which wilds we have, and any remaining cards will give a flush, so there are a total of \({10\choose4}{72\choose2}=536760\) possibilities.
• 5 wilds: There are \(10\choose5\) choices for which wilds we have, and any remaining set of cards will give a flush, so there are a total of \({10\choose5}{72\choose1}=18144\) possibilities.
• 6 wilds: There are \(10\choose6\) possibilities.

So, the total is \(1924944+6952320+8482320+4357440+536760+18144+210=\mathbf{22272138}\).
Back to table

Straights

3 card including a 2

We break it down by the length of the straight:

• 6 card straight: For a 0-5 straight there are \(5\cdot9^5\) possibilities, and for a 1-6 or 2-7 straight there are \(9^6\) possibilities for a total of \(5\cdot9^5+2\cdot9^6=1358127\).
• 5 card straight: For a 0-4 straight there are \(5\cdot9^4\) possibilities and \(82-5-9\) possibilities for the other card (subtracting 5 for the cards used in the straight, and 9 because if the extra card were a 5 that would be a 6 card straight which we counted above). We've overcounted the cases where the other card is a 0-4, so we need to subtract out all straights of 0-4 where the card distribution is (2,1,1,1,1). If 0 has 2 cards there are \({5\choose2}9^4\) of these, and if anywhere from 1-4 has 2 cards there are \({9\choose2}5\cdot9^3\). So for a 0-4 straight there are \(5\cdot9^4(82-5-9)-\left({5\choose2}9^4+4{9\choose2}5\cdot9^3\right)\) possibilities. Using a similar technique, for a 1-5 straight there are \(9^5(82-5-5-9)\) possibilities, but we overcounted the (2,1,1,1,1) distributions so the true number is \(9^5(82-5-5-9)-5{9\choose2}9^4\), and for a 2-6 straight there are \(9^5(82-5-9-9)\) possibilities, but we overcounted the (2,1,1,1,1) distributions so the true number is \(9^5(82-5-9-9)-5{9\choose2}9^4\). This gives us a total of \(5\cdot9^4(82-5-9)-\left({5\choose2}9^4+4{9\choose2}5\cdot9^3\right)+9^5(82-5-5-9)-\left(5{9\choose2}9^4\right)+9^5(82-5-9-9)\left(5{9\choose2}9^4\right)=6482268\).
• 4 card straight: We use the inclusion-exclusion technique as described in the 3 card straight flush, specific suit case. For the 0-3 case our universe of cards is all 82 cards except any 4 (to avoid falling in the 5 card straight case), so there are \(82-9=73\) cards in our universe \(U\). We get \({{73}\choose6}-\left({{73-5}\choose6}+3{{73-9}\choose6}\right)+\left(3{{73-14}\choose6}+3{{73-18}\choose6}\right)-\left(3{{73-23}\choose6}+{{73-27}\choose6}\right)+{{73-32}\choose6}=5452920\). For the 1-4 case our universe is all cards except any 0 or 5, so there are \(82-5-9=68\) cards in our universe. We get \({{68}\choose6}-4{{68-9}\choose6}+6{{68-18}\choose6}-4{{68-27}\choose6}+{{68-36}\choose6}=7488288\). For the 2-5 case our universe is all cards except any 1 or 6, so there are \(82-9-9=64\) cards in our universe, and we get \({{64}\choose6}-4{{64-9}\choose6}+6{{64-18}\choose6}-4{{64-27}\choose6}+{{64-36}\choose6}=6294186\), for a total of \(5452920+7488828+6294186=19235394\).
• 3 card straight: We use inclusion-exclusion again. For a 0-2 straight our universe is all 82 cards except any 3 (to avoid falling in the 4 card straight case), so there are \(82-9=73\) cards in our universe \(U\). So we get \({{73}\choose6}-\left({{73-5}\choose6}+2{{73-9}\choose6}\right)+\left(2{{73-14}\choose6}+{{73-18}\choose6}\right)-{{73-23}\choose6}=14042295\). For a 1-3 straight our universe is everything except 0's and 4's, and there are \(82-5-9=68\) of these. So we get \({{68}\choose6}-3{{68-9}\choose6}+3{{68-18}\choose6}-{{68-27}\choose6}=17456634\). For a 2-4 straight our universe is everything except 1's and 5's, and there are \(82-9-9=64\) of these. So we get \({{64}\choose6}-3{{64-9}\choose6}+3{{64-18}\choose6}-{{64-27}\choose6}=13781016\), for a total of \(14042295+17456634+13781016=45279945\).

So, the total is \(1358127+6482268+19235394+45279945=\mathbf{72355734}\).
Back to table

3 card including a 4

We break it down by the length of the straight:

• 6 card straight: For a 0-5 or 4-9 straight there are \(5\cdot9^5\) possibilities, and for a 1-6, 2-7, or 3-8 straight there are \(9^6\) possibilities for a total of \(2\cdot5\cdot9^5+3\cdot9^6=2184813\).
• 5 card straight: For a 0-4 straight there are \(5\cdot9^4\) possibilities and \(82-5-9\) possibilities for the other card (subtracting 5 for the cards used in the straight, and 9 because if the extra card were a 5 that would be a 6 card straight which we counted above). We've overcounted the cases where the other card is a 0-4, so we need to subtract out all straights of 0-4 where the card distribution is (2,1,1,1,1). If 0 has 2 cards there are \({5\choose2}9^4\) of these, and if anywhere from 1-4 has 2 cards there are \({9\choose2}5\cdot9^3\). So for a 0-4 straight there are \(5\cdot9^4(82-5-9)-\left({5\choose2}9^4+4{9\choose2}5\cdot9^3\right)\) possibilities. Using a similar technique, for a 1-5 (or 4-8) straight there are \(9^5(82-5-5-9)\) possibilities, but we overcounted the (2,1,1,1,1) distributions so the true number is \(9^5(82-5-5-9)-5{9\choose2}9^4\), and for a 2-6 (or 3-7) straight there are \(9^5(82-5-9-9)\) possibilities, but we overcounted the (2,1,1,1,1) distributions so the true number is \(9^5(82-5-9-9)-5{9\choose2}9^4\). This gives us a total of \(5\cdot9^4(82-5-9)-\left({5\choose2}9^4+4{9\choose2}5\cdot9^3\right)+2\left(9^5(82-5-5-9)-\left(5{9\choose2}9^4\right)\right)+2\left(9^5(82-5-9-9)\left(5{9\choose2}9^4\right)\right)=11324286\).
• 4 card straight: We use the inclusion-exclusion technique as described in the 3 card straight flush, specific suit case. For the 1-4 case our universe is all cards except any 0 or 5, so there are \(82-5-9=68\) cards in our universe. We get \({{68}\choose6}-4{{68-9}\choose6}+6{{68-18}\choose6}-4{{68-27}\choose6}+{{68-36}\choose6}=7488288\). For the 2-5 (and 3-6 and 4-7) case our universe is all cards except any 1 or 6, so there are \(82-9-9=64\) cards in our universe, and we get \({{64}\choose6}-4{{64-9}\choose6}+6{{64-18}\choose6}-4{{64-27}\choose6}+{{64-36}\choose6}=6294186\), for a total of \(7488828+3\cdot6294186=26370846\).
• 3 card straight: We use inclusion-exclusion again. For a 2-4 (and 3-5 and 4-6) straight our universe is everything except 1's and 5's, and there are \(82-9-9=64\) of these. So we get \({{64}\choose6}-3{{64-9}\choose6}+3{{64-18}\choose6}-{{64-27}\choose6}=13781016\), for a total of \(3\cdot13781016=41343048\).

So, the total is \(2184813+11324286+26370846+41343048=\mathbf{81222993}\).
Back to table

3 card including a 5

By symmetry this is the same number as 3 card straight including a 4, which is 81222993.
Back to table

3 card including a 7

By symmetry this is the same number as 3 card straight including a 2, which is 72355734.
Back to table

4 card including a 3

We break it down into the length of the straight:

• 6 card straight: For a 0-5 straight there are \(5\cdot9^5\) possibilities, and for a 1-6, 2-7, or 3-8 straight there are \(9^6\) possibilities for a total of \(5\cdot9^5+3\cdot9^6=1889568\).
• 5 card straight: For a 0-4 straight there are \(5(9^4)\) possibilities for the straight and \(82-5-9\) possibilities for the other card (we subtract 5 for the 5 cards used in the straight, and 9 because if the extra card were a 5 that would be a 6 card straight which we counted above). However, we've overcounted the cases where the other card is a 0-4. So we need to subtract out all straights of 0-4 where the card distribution is (2,1,1,1,1). If 0 has 2 cards there are \({5\choose2}9^4\) of these, and if anywhere from 1-4 has 2 cards there are \(5{9\choose2}9^3\). So for a 0-4 straight there are \(5\cdot9^4(82-5-9)-({5\choose2}9^4+4{9\choose2}5\cdot9^3)\) possibilities. Using a similar technique, for a 1-5 straight there are \(9^5(82-5-5-9)\) possibilities, but we overcounted the (2,1,1,1,1) distributions so the true number is \(9^5(82-5-5-9)-5{9\choose2}9^4\). For a 2-5 straight (and similarly a 3-6 straight) there are \(9^5(82-5-9-9)-5{9\choose2}9^4\) possibilities. This gives us a total of \(5\cdot9^4(82-5-9)-\left({5\choose2}9^4+4{9\choose2}5\cdot9^3\right)+9^5(82-5-5-9)-5{9\choose2}9^4+2\left(9^5(82-5-9-9)-5{9\choose2}9^4\right)=8785179\).
• 4 card straight: We break it down again by the type of straight:
  • 0-3: There are \(5(9^3)\) possibilities for the straight and \({82-4-9}\choose2\) possibilities for the other two cards (excluding the cards we already chose and any 4's since that would make it a 5 card straight). However, again we've overcounted cases where the extra cards are 0-3. The distributions of cards we have to exclude are (2,1,1,1), (3,1,1,1), and (2,2,1,1). For (2,1,1,1), if 0 has 2 cards there are \({5\choose2}9^3\) possibilities and if anywhere from 1-3 has 2 cards there are \({9\choose2}5\cdot9^2\) possibilities. In either case, there are \(82-5-9\cdot4\) possibilities for the extra card, since the extra card can't be anywhere from 0-4, to avoid changing the distribution or making it a 5 card straight. For (3,1,1,1), if 0 has 3 cards there are \({5\choose3}9^3\) possibilities and otherwise there are \({9\choose3}5\cdot9^2\) possibilities. For (2,2,1,1), if 0 has 2 cards there are \({5\choose2}3{9\choose2}9^2\) possibilities and otherwise there are \({9\choose2}{9\choose2}5\cdot9\) possibilities. Note that we have to subtract 2 times the number of (3,1,1,1) overcounting (since we've counted these \(3\cdot1\cdot1\cdot1\) times and we want to only count them once) and 3 times the number of (2,2,1,1) overcounting. This gives us a total of \( \begin{array}{lll} 5\cdot9^3{{82-4-9}\choose2} & - ({5\choose2}9^3+3{9\choose2}5\cdot9^2)(82-5-9\cdot4) & \\ & - 2({5\choose3}9^3+3{9\choose3}5\cdot0^2) & \\ & - 3({5\choose2}3{9\choose2}9^2+{3\choose2}{9\choose2}{9\choose2}5\cdot9 & = 5452920 \end{array} \)
  • 1-4: We use a similar technique as the 0-3 case. There are \(9^4\) possibilities for the straight and \({{82-4-5-9}\choose2}\) possibilities for the other cards (excluding the cards we chose and 0's and 5's to avoid 5 card straights). For the (2,1,1,1) distribution there are \(4{9\choose2}9^3\) possibilities and \(82-5-9\cdot5\) possibilities for the extra card (avoiding any numbers from 0-5). For the (3,1,1,1) distribution there are \(4{9\choose3}9^3\) possibilities and for the (2,2,1,1) distribution there are \({4\choose2}{9\choose2}{9\choose2}9^2\) possibilities. This gives us a total of \( \begin{array}{lll} 9^4{{82-4-5-9}\choose2} & - (4{9\choose2}9^3)(82-5-9\cdot5) & \\ & - 2(4{9\choose3}9^3) & \\ & - 3({4\choose2}{9\choose2}{9\choose2}9^2 & = 7488288 \end{array} \)
  • 2-5 (and similarly 3-6): We use a similar technique as the 0-3 case. There are \(9^4\) possibilities for the straight and \({{82-4-9-9}\choose2}\) possibilities for the other cards (excluding the cards we chose and 1's and 6's to avoid 5 card straights). For the (2,1,1,1) distribution there are \(4{9\choose2}9^3\) possibilities and \(82-9\cdot6\) possibilities for the extra card (avoiding any numbers from 1-6). For the (3,1,1,1) distribution there are \(4{9\choose3}9^3\) possibilities and for the (2,2,1,1) distribution there are \({4\choose2}{9\choose2}{9\choose2}9^2\) possibilities. This gives us a total of \( \begin{array}{lll} 9^4{{82-4-9-9}\choose2} & - (4{9\choose2}9^3)(82-9\cdot6) & \\ & - 2(4{9\choose3}9^3) & \\ & - 3({4\choose2}{9\choose2}{9\choose2}9^2 & = 6294186 \end{array} \)

So, the total is \(1889568+8785179+5452920+7488288+2\cdot6294186=\mathbf{36204327}\).
Back to table

4 card including a 6

By symmetry this is the same number as 4 card straight including a 3, which is 36204327.
Back to table

5 card

We break it down into the length of the straight:

• 6 card straight: To make a 0-5 straight, there are \(5\cdot9^5\) possibilities (and the same number for a 4-9 straight), and for 1-6 there are \(9^6\) for a total of \(2(5\cdot 9^5)+3(9^6)=2184813\).
• 5 card straight: For a 0-4 straight, there are \(5\cdot9^4\) ways. There are \(82-5-9\) ways to choose the next card (to avoid ones we've already chosen and to avoid making a 6 card straight). However, this double counts cases with a (2,1,1,1,1) distribution of cards over 0-4, so we have to subtract those - there are \({5\choose2}9^4\) where we have 2 0's and \(4({9\choose2}5\cdot9^3)\) where we have 2 of something else. We use a similar technique to count the rest of the straights, giving us a total of \begin{eqnarray*} 2[(5\cdot9^4)(82-5-9)-({5\choose2}9^4+4({9\choose2}5\cdot9^3))] & & \\ +2(9^5(82-5-9-5)-5{9\choose2}9^4) & &\\ +2(9^5(82-5-9-9)-5{9\choose2}9^4) & = & 12964536 \end{eqnarray*}

So, the total is \(2184813+12964536=\mathbf{15149349}\).
Back to table

Straight Flushes

3 card, specific suit

Since we're dealing in a specific suit (let's say G(reen)), there are 3 cards of that suit (including 1 wild) for each number except 0 and 9, and there are 2 cards for those. We break it down by the length of the straight flush:

• 6 card straight flush: For a 0-5 or 4-9 straight there are \(2\cdot3^5\) possibilities and for a 1-6, 2-7, or 3-8 straight there are \(3^6\) possibilities for a total of \(2(2\cdot3^5)+3(3^6)=3159\).
• 5 card straight flush: For a 0-4 straight, there are \(2\cdot3^4\) ways to choose the straight, and \(82-5-3\) ways to choose the next card (to avoid cards we've already chosen and to avoid making a 6 card straight). However, this double counts cases with a (2,1,1,1,1) distribution of cards over 0-4, so we have to subtract those - there are \({2\choose2}3^4\) where we have 2 0's and \(4{3\choose2}2\cdot3^3\) where we have 2 of something else. We use a similar technique to count the rest of the straights, giving us a total of \begin{eqnarray*} 2\left[(2\cdot3^4)(82-5-3)-\left({2\choose2}3^4+4{3\choose2}2\cdot3^3\right)\right] & & \\ +2\left[3^5(82-5-2-3)-5{3\choose2}3^4\right] & & \\ +2\left[3^5(82-5-3-3)-5{3\choose2}3^4\right] & = & 87156 \end{eqnarray*}
• 4 card straight flush: We could use a similar technique to the 5 card case (like we do in the 4 card straight including a 3 case). However, let's try something different and use the Inclusion-exclusion principle. For the 0-3 case, our universe of cards is all 82 cards except for any Green 4 (to avoid falling in the 5 card straight flush case), so there are \(82-3=79\) cards in our universe \(U\). Let \(A_0\) be the set of hands that don't have a Green 0, \(A_1\) be the set of hands that don't have a Green 1, up to \(A_3\) being the set of hands that don't have a Green 3. Then what we want is the set of hands that satisfy none of \(A_0, \ldots A_4\), or \(\left|\bigcap \overline{A_i}\right|\), which by de Morgan's laws is \(\left|\overline{\bigcup A_i}\right|=\left|U\right|-\left|\bigcup A_i\right|\). Now, \(\left|A_0\right|\) is the number of hands that don't have a Green 0, which is \({{79-2}\choose6}\), and the other \(\left|A_i\right|\)'s are \({{79-3}\choose6}\). \(\left|A_0\cap A_i\right|\) is the number of hands that don't have a Green 0 or a Green \(i\), which is \({{79-2-3}\choose6}\), and the other \(\left|A_i\cap A_j\right|\)'s are \({{79-3-3}\choose6}\). We continue on in this manner to find that the number of 4 card straight flushes of numbers 0-3 is \({{79}\choose6}-\left[{{79-2}\choose6}+3{{79-3}\choose6}\right]+\left[3{{79-5}\choose6}+3{{79-6}\choose6}\right]-\left[3{{79-8}\choose6}+{{79-9}\choose6}\right]+{{79-11}\choose6}=136161\) (and by symmetry this is the number of 4 card straight flushes 6-9). We use a similar technique (letting our universe of cards be all 82 cards except Green 0's and Green 5's) to calculate the number of 4 card straight flushes of numbers 1-4 (and 5-8 by symmetry) is \({{77}\choose6}-4{{77-3}\choose6}+6{{77-6}\choose6}-4{{77-9}\choose6}+{{77-12}\choose6}=190134\). Again, letting our universe be all 82 cards except Green 1's and Green 6's, the number of 4 card straight flushes of numbers 2-5 (and 3-6 and 4-7 by symmetry) is \({{76}\choose6}-4{{76-3}\choose6}+6{{76-6}\choose6}-4{{76-9}\choose6}+{{76-12}\choose6}=184626\), which gives us a total of \(2\cdot136161+2\cdot190134+3\cdot184626=1206468\).
• 3 card straight flush: We use a similar technique as above, although we have to consider the case where we have two non-adjacent 3 card straight flushes separately. Notice that under this technique, the expressions get simpler the fewer cards we have, unlike the technique of subtracting off distributions we overcounted which gets more complicated the fewer cards we have. For 0-2, our universe of cards is 82-3=79, so we get \({{79}\choose6}-\left[{{79-2}\choose6}+2{{79-3}\choose6}\right]+\left[2{{79-5}\choose6}+{{79-6}\choose6}\right]-{{79-8}\choose6}=1144050\), although we have to subtract the two non-adjacent 3 card straight flushes which is \((2\cdot3^2)(3\cdot3^3+2\cdot3^2)=1782\). (these are the same as 7-9 by symmetry) For 1-3 (and by symmetry 6-8) our universe of cards is 82-5=77, so we get \({{77}\choose6}-3{{77-3}\choose6}+3{{77-6}\choose6}-{{77-9}\choose6}=1545075\), then subtracting \(3^3(2\cdot3^3+2\cdot3^2)=1944\). For 2-4 (and 5-7) our universe of cards is 82-6=76, so we get \({{76}\choose6}-3{{76-3}\choose6}+3{{76-6}\choose6}-{{76-9}\choose6}=1479843\), then subtracting \(3^3(3^3+2\cdot3^2)=1215\). For 3-5 (and 4-6) our universe of cards is 82-6=76, so we get \({{76}\choose6}-3{{76-3}\choose6}+3{{76-6}\choose6}-{{76-9}\choose6}=1479843\), then subtracting \(3^3(2\cdot3^2)=486\). Finally, we have to add in the case where there are two non-adjacent 3 card straights. If the first straight is 0-2, the other straight could be anywhere from 4-6 to 7-9, which gives \(2\cdot3^2(3\cdot3^3+2\cdot3^2)\). Adding up all such cases gives an additional \(2\cdot3^2(3\cdot3^3+2\cdot3^2)+3^3(2\cdot3^3+2\cdot3^2)+3^3(3^3+2\cdot3^2)+3^3(2\cdot3^2)=5427\) possibilities. This gives a total of \(2(1144050-1782)+2(1545075-1944)+2(1479843-1215)+2(1479843-486)+5427=11292195\).

So, the total is \(3159+87156+1206468+11292195=\mathbf{12588978}\).
Back to table

3 card, any suit

You can perhaps do some sort of inclusion-exclusion argument where your sets are the hands that have 3 cards in any particular suit, but it gets very complicated very fast - open to suggestions.
Back to table

4 card, any suit

You can perhaps do some sort of inclusion-exclusion argument where your sets are the hands that have 4 cards in any particular suit, but it gets very complicated very fast - open to suggestions.
Back to table

Poker Hands

2 pair

We can make two pair by all the possibilities under Full House, plus the following:

• 2-2-2 split (i.e. three pairs): If we use the numbers 0 and 9, there are \({5\choose2}{5\choose2}\) for the choices of the cards of number 0 and 9, 8 choices for the other number, and \({9\choose2}\) choices for the cards of that number. If we use only one of 0 and 9, there are 2 choices for which one to use, \({5\choose2}\) choices for the cards of that number, \({8\choose2}\) choices for the other two numbers, and \({9\choose2}\) choices for the cards in each number. If we use neither 0 nor 9, there are \(8\choose3\) choices for the numbers and \({9\choose2}\) for the cards in each number. This gives a total of \({5\choose2}{5\choose2}\cdot8{9\choose2}+2{5\choose2}{8\choose2}{9\choose2}{9\choose2}+{8\choose3}{9\choose2}{9\choose2}{9\choose2}=3367296\).
• 2-2 split with no other pair: If we use 0 and 9, there are \({5\choose2}{5\choose2}\) possibilities for those cards. For the other two cards, they can't be 0 or 9, so there are \({{82-5-5}\choose2}\) choices, except \(8{9\choose2}\) of these lead to another pair, so we subtract them. Similarly, if we use one of 0 and 9, there are \(2{5\choose2}8{9\choose2}({{82-5-9}\choose2}-(7{9\choose2}+{5\choose2}))\) choices and if we use neither 0 nor 9 there are \({8\choose2}{9\choose2}{9\choose2}({{82-9-9}\choose2}-(6{9\choose2}+2{5\choose2}))\) for a total of \({5\choose2}{5\choose2}({{82-5-5}\choose2}-8{9\choose2})+ 2{5\choose2}8{9\choose2}({{82-5-9}\choose2}-(7{9\choose2}+{5\choose2}))+ {8\choose2}{9\choose2}{9\choose2}({{82-9-9}\choose2}-(6{9\choose2}+2{5\choose2}))=76431600\).

So, the total is \(12646280+3367296+76431600=\mathbf{92445176}\).
Back to table

3 of a kind

We break it down by the number of cards of the same number:

• 6 of a kind: Since there are only 5 0's and 9's, we must be a 1-8, so there are 8 choices for the number and \({9\choose6}\) ways to choose the cards of that number for a total of \(8{9\choose6}=672\).
• 5 of a kind: If the number is 0 or 9, there are \({5\choose5}\) ways to choose the cards of that number and \(82-5\) ways to choose the other card. Otherwise, there are \({9\choose5}\) ways to choose the cards of that number and \(82-9\) (to avoid picking the same number again) to choose the other card. This gives a total of \(2{5\choose5}(82-5)+8{9\choose5}(82-9)=73738\).
• 4 of a kind: If the number is 0 or 9, there are \({5\choose4}\) ways to choose the cards of that number and \({82-5}\choose2\) ways to choose the other card. Otherwise, there are \({9\choose4}\) ways to choose the cards of that number and \({82-9}\choose2\) ways to choose the other card. This gives a total of \(2{5\choose4}{{82-5}\choose2}+8{9\choose4}{{82-9}\choose2}=2678284\).
• 3 of a kind and 3 of another kind: (we break this out separately to avoid overcounting) - we count this in the Full house section, and the result is 211108.
• 3 of a kind (and not 3 of another kind): If the number is 0 or 9, there are \(5\choose3\) ways to choose the cards of that number and \({{82-5}\choose3}\) ways to choose the other cards, but we have to subtract off the number of ways to choose another 3 of a kind, which is \({5\choose3}+8{9\choose3}\). Otherwise, there are \(9\choose3\) ways to choose the cards of that number and \({{82-9}\choose3}\) ways to choose the other cards, but again we subtract \(2{5\choose3}+7{9\choose3}\), which is the number of ways to choose another 3 of a kind. This gives us a total of \(2{5\choose3}\left({{82-5}\choose3}-\left({5\choose3}+8{9\choose3}\right)\right)+8{9\choose3}\left({{82-9}\choose3}-\left(2{5\choose3}+7{9\choose3}\right)\right)=42836496\).

So, the total is \(672+73738+2678284+211108+42836496=\mathbf{45800298}\).
Back to table

Full house

We break it down by the distribution of cards in the full house:

• 4 of one number and 2 of another: If the number of the 4 cards is 0 or 9, there are 2 choices for the number, \(5\choose4\) ways to choose the cards in that number and \(8{9\choose2}+{5\choose2}\) ways to choose the cards in the other number. If the number of the 4 cards is not 0 or 9, there are 8 choices for the number, \(9\choose4\) ways to choose the cards in that number and \(7{9\choose2}+2{5\choose2}\) ways to choose the cards in the other number. This gives a total of \(2{5\choose4}(8{9\choose2}+{5\choose2})+8{9\choose4}(7{9\choose2}+2{5\choose2})=277156\).
• 3 of one number and 3 of another: If the numbers are 0 and 9, there are \({5\choose3}{5\choose3}\) choices. If one of the numbers is 0 or 9, there are \(2{5\choose3}\cdot8{9\choose3}\) choices. If neither number is 0 nor 9, there are \({8\choose2}\) ways to choose the numbers, so there are \({8\choose2}{9\choose3}{9\choose3}\) choices. All together, this gives \({5\choose3}{5\choose3}+2{5\choose3}\cdot8{9\choose3}+{8\choose2}{9\choose3}{9\choose3}=211108\).
• 3 of one number and 2 of another: If the number of the 3 cards is 0 or 9, there are 2 choices for the number, \({5\choose3}\) choices for the cards in that number, and \(8{9\choose2}(82-5-9)+{5\choose2}(82-5-5)\) for the other 3 cards. If the number of the 3 cards is not 0 or 9, there are 8 choices for the number, \({9\choose3}\) choices for the cards in that number, and \(7{9\choose2}(82-9-9)+2{5\choose2}(82-9-5)\) choices for the other 3 cards. All together, this gives \(2{5\choose3}(8{9\choose2}(82-5-9)+{5\choose2}(82-5-5))+8{9\choose3}(7{9\choose2}(82-9-9)+2{5\choose2}(82-9-5))=12158016\).

So, the total is \(277156+211108+12158016=\mathbf{12646280}\).
Back to table

Miscellaneous

5 odd cards

We break it down by the number of odd cards:

• 6 odd cards: There are 41 odd cards, so there are \({41\choose6}=4496388\) possibilities.
• 5 odd cards: There are also 41 even cards, so there are \({41\choose5}41=30725318\) possibilities.

This gives a total of \(4496388+30725318=\mathbf{35221706}\).
Back to table

5 even cards

Since there are 41 even cards and 41 odd cards, by symmetry this is the same number as 5 odd cards, which is 35221706.
Back to table

3 cards totalling \(\leq 4\)

We break it down by the lowest two cards in the hand:

• 0 and 0: Firstly, we count how many hands have 0 and 0 as their lowest cards. There are \({82}\choose6\) total hands, \({82-5}\choose6\) hands that have no 0 cards, and \(5{{82-5}\choose5}\) hands with only 1 0, so the number of hands that have 0 and 0 as their lowest cards is \({{82}\choose6}-\left({{82-5}\choose6}+5{{82-5}\choose5}\right)\). Of these, the only hands that don't have 3 cards totalling \(\leq 4\) are those that only have 5's or higher for the remaining cards, and there are \({5\choose2}{{82-5-9\cdot4}\choose4}\) of these, so our total is \({{82}\choose6}-\left({{82-5}\choose6}+5{{82-5}\choose5}\right)-{5\choose2}{{82-5-9\cdot4}\choose4}=13266257\).
• 0 and 1: There are 5 choices for which 0 we have, and for the remaining 5 cards there are \({82-5}\choose5\), and \({82-5-9}\choose5\) have no 1's, so the number of these hands is \(5\left({{82-5}\choose5}-{{82-5-9}\choose5}\right)\). Of these, the only hands that don't have 3 cards totalling \(\leq 4\) are those that only have 4's or higher for the remaining cards, and there are \(5\cdot9{{82-5-9\cdot3}\choose4}\) of these, so our total is \(5\left({{82-5}\choose5}-{{82-5-9}\choose5}\right)-5\cdot9{{82-5-9\cdot3}\choose4}=36304935\).
• 0 and 2: There are 5 choices for which 0 we have, and for the remaining 5 cards (which have no 1's) there are \({82-5-9}\choose5\), and \({82-5-9\cdot2}\choose5\) have no 1's, so the number of these hands is \(5\left({{82-5-9}\choose5}-{{82-5-9\cdot2}\choose5}\right)\). Of these, the only hands that don't have 3 cards totalling \(\leq 4\) are those that only have 3's or higher for the remaining cards, and there are \(5\cdot9{{82-5-9\cdot2}\choose4}\) of these, so our total is \(5\left({{82-5-9}\choose5}-{{82-5-9\cdot2}\choose5}\right)-5\cdot9{{82-5-9\cdot2}\choose4}=6608040\).
• 1 and 1: There are \({82-5}\choose6\) hands that have no 0's, but \({82-5-9}\choose6\) of these hands have no 1's, and \(9{{82-5-9}\choose5}\) of these hands have exactly 1 1. So, there are \({{82-5}\choose6}-\left({{82-5-9}\choose6}+9{{82-5-9}\choose5}\right)\) hands that have 1 and 1 as their lowest cards. Of these, the only hands that don't have 3 cards totalling \(\leq 4\) are those that only have 3's or higher for the remaining cards, and there are \({9\choose2}{{82-5-9\cdot2}\choose4}\) of these, so our total is \({{82-5}\choose6}-\left({{82-5-9}\choose6}+9{{82-5-9}\choose5}\right)-{9\choose2}{{82-5-9\cdot2}\choose4}=17438748\).

Therefore, the total number is \(13266257+36304935+6608040+17438748=\mathbf{73617980}\).
Back to table

3 cards totalling \(\geq 23\)

By symmetry this is the same number as 3 cards totalling \(\leq 4\), which is 73617980.
Back to table

Skip straight

A skip straight is a 4 card straight where there's a 1 number gap between each card: i.e. 0 2 4 6, 1 3 5 7, etc.
We break it down by the length of the skip straight:

• 5 card skip straight: The possibilities are 0 2 4 6 8 and 1 3 5 7 9. For 0 2 4 6 8, there are \(5\cdot9^4\) possibilities for the straight and \(82-5\) possibilities for the extra card. However, this double counts cases with a (2,1,1,1,1) distribution of cards in the straight. If there are 2 0's, there are \({5\choose2}9^4\) possibilities, and if there are 2 of anything else there are \({9\choose2}5\cdot9^3\) possibilities. This gives us a total of \(5\cdot9^4(82-5)-\left({5\choose2}9^4+4{9\choose2}5\cdot9^3\right)=1935495\), and by symmetry the same total for 1 3 5 7 9.
• 4 card skip straight: We use the inclusion-exclusion technique as described in the 3 card straight flush, specific suit case. For 0 2 4 6 (and similarly 3 5 7 9), our universe of cards is all 82 cards except any 8 (to avoid falling in the 5 card skip straight case), so there are \(82-9=73\) cards in our universe \(U\). We get \({{73}\choose6}-\left({{73-5}\choose6}+3{{73-9}\choose6}\right)+\left(3{{73-14}\choose6}+3{{73-18}\choose6}\right)-\left(3{{73-23}\choose6}+{{73-27}\choose6}\right)+{{73-32}\choose6}=5452920\).
  For 1 3 5 7 (and similarly 2 4 6 8), our universe of cards is all 82 cards except any 9, so there are \(82-5=77\) cards in our universe \(U\). We get \({{77}\choose6}-4{{77-9}\choose6}+6{{77-18}\choose6}-4{{77-27}\choose6}+{{77-36}\choose6}=10558836\).

So, our total is \(2\cdot1935495+2\cdot5452920+2\cdot10558836=\mathbf{35894502}\).
Back to table

Mixed straight

A mixed straight is a 4 card straight in which each of the cards is a different suit. I'm open to suggestions on how to count this efficiently.
Back to table

About this project

This page uses MathJax to translate LaTeX into HTML.

• calculateprobs.py is the Python script that calculates the exact number of 6 card hands that satisfy each target card. I was intending to use it as just a check on my by-hand calculations, but as the combinatorics got harder and harder I used it as the only calculation for a few target cards.
• outputgraph.py generates the pretty graph of target cards. It uses matplotlib.

A previous version of this page was generated directly from the LaTeX file - you can view it here.