Super Mario Bros. (board game) Solver

About this project: A friend of mine showed me the Super Mario Bros. board game. It's clearly designed for kids, but I was posed an interesting question: what's the probability of winning on the first turn?

Well, it's not that interesting, but still. Each roll has a 1/3 chance of moving one space, 1/3 chance of moving two spaces, 1/6 chance of moving one or two spaces (your choice), and 1/6 chance of having to end your turn...unless you have 4 coins to spend to get an extra life. You also end your turn if you land in an obstacle such as water or fire. Here's a good picture of the game board.

So, as you can see in the Python script used to calculate the results, the main recursive part is pretty straightforward.

Results

Here are the probabilities of winning a game on the first turn under the following conditions:

Conditions	Probability
Normal	.77766475% (1 in 129)
Ignoring obstacles	7.73834380% (1 in 12.9)
Not picking up coins	.00000656% (1 in 15238260)
Not picking up coins and ignoring obstacles	.00318851% (1 in 31362)
Starting with 4 coins	2.07943427% (1 in 48.1)
Starting with 8 coins	4.07525193% (1 in 24.5)
Starting with 13 coins	7.94019973% (1 in 12.6)
Starting with 38 coins	51.23511673% (1 in 2.0)

So, you have a 1 in 129 chance of winning on the first turn, which is a lot better than I had expected. Ignoring obstacles is a pretty big help, about equivalent to starting with 13 coins. You have to start with 38 coins to get more than a 50% chance to win on the first turn.

Here's a graph illustrating the effect of starting with coins (generated with Gnuplot from this script):

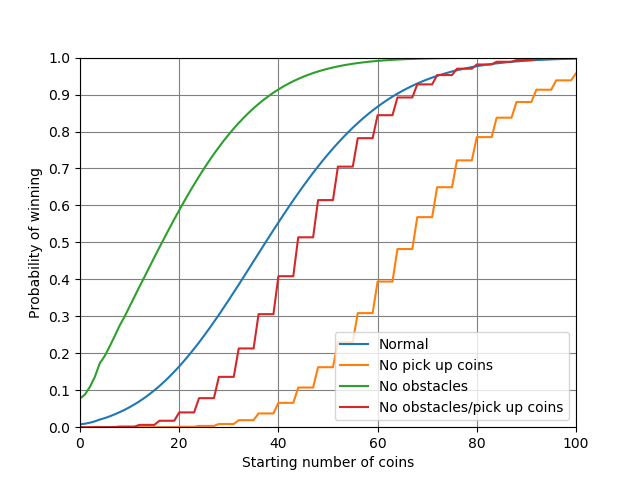
The stair-stepping effect happens because if you don't pick up any coins, starting with 3 is no better than starting with 0 (since every 4 is a free life).

Here's a graph of your probability of winning depending on what square you're on (and how many coins you have), generated from this script. The faint vertical lines indicate squares with obstacles.

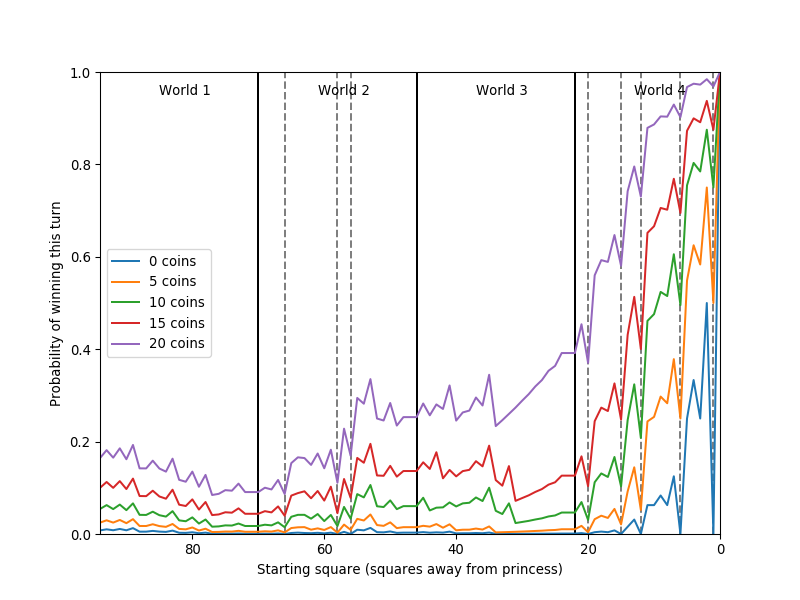
It's interesting that your probability of winning actually goes down through World 1, presumably because there are a lot of coins and mushrooms you should be getting.